One-way Analysis of Variance (ANOVA)
- Hussam Omari
- 12 فبراير 2023
- 5 دقيقة قراءة

In the previous article, we explained the concept, usage, and results interpretation of student's t-test. The student’s t-test is a type of inferential statistics used to determine if there is a significant difference between the means of two groups, whereas Analysis of Variance (ANOVA) is used to determine if there is a significant difference between the means of more than two groups. To use the ANOVA test, our data must meet the following assumptions:
Each group sample is drawn randomly from a normally distributed population
All populations have a common variance
All samples are drawn independently of each other
There should be no significant outliers.
Factor effects are additive.
One-way vs Two-way ANOVA
There are different versions of ANOVA are used depending on the design of a study. a one-way ANOVA is used when only one independent variable is tested in the experiment, whereas a two-way ANOVA is used with two independent variables.
Suppose we conducted a study about spraying three concentrations of a growth stimulant (2, 4, and 6 ml/l) on corn plants. Later, we measured the height of each plant sprayed with specific concentration of the three. The plant height in this experiment is considered the dependent variable because the plants height values are affected by the the growth stimulant concentrations, whereas the growth stimulant itself is considered the independent variable which is also known as "factor".
In addition, each concentration is considered a factor level and in this example we have 3 factor levels (3 concentrations), therefore we have 3 plant groups; each group received similar concentration (Figure 1).
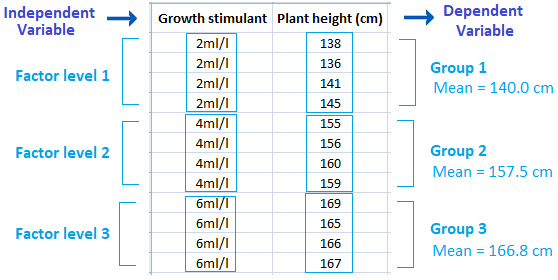
Figure 1: Independent and dependent variable illustration
Note that the independent variable (growth stimulant) is not a measurement, as in plant height. The independent variable is a factor that manipulates or affect the independent variable. Therefore, in this study, the plant height measurement is considered a response to the growth stimulant concentrations effect.
In two-way ANOVA, we have two independent variables that both manipulate e dependent variable. Suppose we conducted a study about spraying three concentrations of a growth stimulant (2, 4, and 6 ml/l) on corn plants, and in the same time these plants were grown in three different type of soils. The measurement taken throughout the study was plant height. In this experiment, we have one dependent variable (plant height) and two independent variables (two treatments); the growth stimulant and the type of soil.
The F Statistic
The F distributions, named after the statistician and geneticist R. A. Fisher, are probability distributions that are used in many kinds of statistical analysis. The F statistic forms the basis for ANOVA.
We calculate F statistic (F-obtained), which we compare to F-tabulated (obtained from F distribution table), to determine whether any of the means represent different. When F is not significant, it indicates no significant differences between the means. Then the experiment has failed to demonstrate a relationship.
Many statistical analysis software compute F and p-value for us, and depending on the p-value, we can decide if there is a significant difference existed between groups or not. The p-value is a probability that measures the evidence against the null hypothesis. For most researches, the p-value is set at 0.05, whereas in medical researches that involve experiments on human the p-value is set at 0.01 level of significance.
In summary, the F statistic and its p-value only indicate if a significant difference between groups' means is existed or not, but it doesn't tell us which of the groups significantly differs from the other groups.
Hypotheses Testing in ANOVA
Unlike t-test, ANOVA tests are only two-tailed hypotheses and its hypothesis test is usually takes the following formula:

The H0 is the null hypothesis and indicates that there is no significant difference between groups' means, whereas the Ha is the alternative hypothesis and indicates that at least one of the groups means under study are significantly differ from other groups means.
When our p-value is smaller than the alpha level that previously defined (often, 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis.
Post Hoc Tests
As we mentioned previously, ANOVA is used to determine if a significant difference between the means of three groups or more is existed or not. However, F statistic in ANOVA doesn't tell us which of the groups significantly differs from the other groups, therefore we need further tests that help us to detect which means are significantly differ from other means' groups; this kind of test are known as post hoc tests.
Post hoc tests are like t-tests in which we compare all possible pairs of means from a factor, one pair at a time, to determine which means differ significantly. The most common post hoc tests are the following:
Fisher's Least Significant Difference (LSD)
Duncan's new multiple range test (MRT)
Dunn's Multiple Comparison Test.
Holm-Bonferroni Procedure.
Scheffé's Method.
Tukey's test
Comprehensive Example
Let's bring and analyze the growth stimulant data of the previously mentioned example. The study was conducted to measure the effect of a growth stimulant on corn plants. Corn plants were sprayed with three concentrations of a growth stimulant (2, 4, and 6 ml/l). At the end of the experiment, we measured the height of each plant that were sprayed with specific concentration of the three.
In this study example, we have one independent variable (growth stimulant) with three factor levels (concentrations), therefore we can analyze data using one-way ANOVA and post hoc test (e.g. LSD) to determine if there is a significant difference between the means of the three groups. The Figure 2 helps to visualize and explore groups' means sprayed with specific concentration.

Figure 2: Plant groups' means sprayed with specific concentration
The ANOVA Results
The ANOVA results presented in Figure 3 are obtained using SAS software. Notice that the p-value of the F value is less than the critical value (0.05). Therefore, we reject the null and accept the alternative hypothesis which indicates that at least one of the groups' mean under study are significantly differ from other groups' means.

Figure 3: ANOVA table of the effect of a growth stimulant on corn plants
Since the F value is significant, we can now compare the mean values using post-hoc (LSD) test as shown in Figure 4 results. Notice that each plants group' mean is denoted with a subscription letter (A, B, or C), and since each mean has different letter, this indicates a significant difference between the mean and the other means. Also, the highest mean values is denoted with A letter, while the lesser mean values are denoted with C and so on. However, in statistics, if two means or more were denoted with same letter, these means are statistically equal and there is no significant difference between them.

Figure 4: Post hoc (LSD) results of the effect of a growth stimulant on corn plants
Results Visualization and Interpretation
Now, we can use data visualization such as a bar-chart or a table to show the groups means denoted with a significant difference subscriptions (alphabet letters) as shown in Figure 5.

Figure 5: Plant groups' means sprayed with specific concentration
The results of the study indicated that corn plant sprayed with 6ml/l showed a significant higher increase in plant height compared to all other plants under study. In addition, plants sprayed with 4ml/l showed significantly higher height than plants sprayed with 2ml/l.
References
Mendenhall, W. M., & Sincich, T. L. (2016). Statistics for Engineering and the Sciences Student Solutions Manual (6th ed.). USA: Taylor & Francis Group, LLC.
Heiman, G. W. (2011). Basic Statistics for the Behavioral Sciences (6th ed.). USA: Cengage Learning.
Samuels, M. L., Witmer, J. A., & Schaffner, A. (2012). Statistics for the Life Sciences (4th ed.): Pearson Education, Inc.
Weiss, N. A., & Weiss, C. A. (2012). Introductory Statistics (9th ed.): Pearson Education, Inc.

















تعليقات